What Is The Learning Rate In Neural Network

Learning Rates for Neural Networks

Evolution of non adaptive learning rates over fourth dimension — Research review series

Function ane : Cyclical Learning Rates for Grooming Neural Networks

This is the first post in the series of posts covering evolution of Non-adaptive learning rate techniques. Each post reviews i prominent paper in that area.

Let's start with kickoff installment of the serial reviewing "Cyclical Learning Rates for Preparation Neural Networks"

In search for a moment of tranquility, Chandratal lake, Himachal Pradesh. (photo courtesy)

Introduction

Grooming a neural network from scratch can exist an intimidating job for many, because there are dozens of tuning knob which has to be set properly to surpass or even to achieve human level accuracy.

Although the mundane job of learning the parameter are done by the network architecture (with the help of gradient descent and back-propagation) much more than challenging task of finding the right hyper parameter is left to u.s.a.. Ane such important hyper parameter is Learning Rate, so in this postal service and upcoming series of posts you volition run across some of the major breakthroughs done in non-adaptive learning rate techniques. Y'all may ask why non-adaptive learning rate particularly, because in that location are many blog mail which has washed extensive adaptive learning rate reviews IMHO.

(This blog post assumes that the reader is familiar with Stochastic Gradient Descent and Learning Rate Decay).

Learning Charge per unit — Primer.

Learning charge per unit is one of the most important hyper parameter to be tuned and holds key to faster and effective training of Neural Networks. Learning charge per unit decides how much of the mistake value has to be dorsum propagated to the weights in the network in gild to move in the direction of lower loss.

Formally information technology looks something like this,

new_weight = existing_weight - learning_rate * gradient

And so, what's with these learning rate ?

Learning rate is 1 of the most tricky hyper parameter. If the learning charge per unit is set very loftier, loss overshoots and diverges otherwise if it's prepare to a very low value then it would take forever to reach the optimum point. Take hold of here is to fix the right learning rate which glides through the loss, something like the red line in the below film.

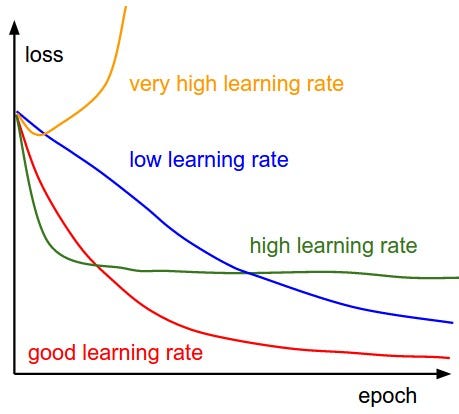
Figure 1. Effects of dissimilar learning rates. (paradigm credits)

Flick's fine but would be the optimal learning charge per unit in numbers ?? Andrej's tweet about learning rate,

Okay ! but seriously ? ane learning rate works all-time for all learning problems and architecture ??

Not really.,

And then there is no one skilful value for learning rate to railroad train neural networks. In this post you will see one prominent technique without the math backside it 😇.

Cyclical Learning Rate for Grooming Neural Networks.

This paper from Leslie N. Smith was an interesting one, which is completely different from adaptive learning rate techniques at the fourth dimension of his writing.

"Instead of monotonically decreasing the learning rate, cyclical learning rate method lets the learning rate cyclically vary between reasonable boundary values"

so this is the basic thought of this Cyclical Learning Charge per unit(CLR) technique.

To dig deeper, traditional wisdom motivates that the learning rate should be one fixed value that that monotonically decreases during (learning rate disuse or annealing) training. Just this newspaper argues and proves that learning charge per unit couldn't be one single value rather it takes on value within a range in a cyclical manner. Training CIFAR-10 dataset with fixed learning charge per unit took around seventy,000 iterations to achieve an accuracy of 81.four% but with this Cyclical Learning Rate technique the same accuracy could be accomplished inside 25,000 iterations which is less than half of the fixed learning rate setting.

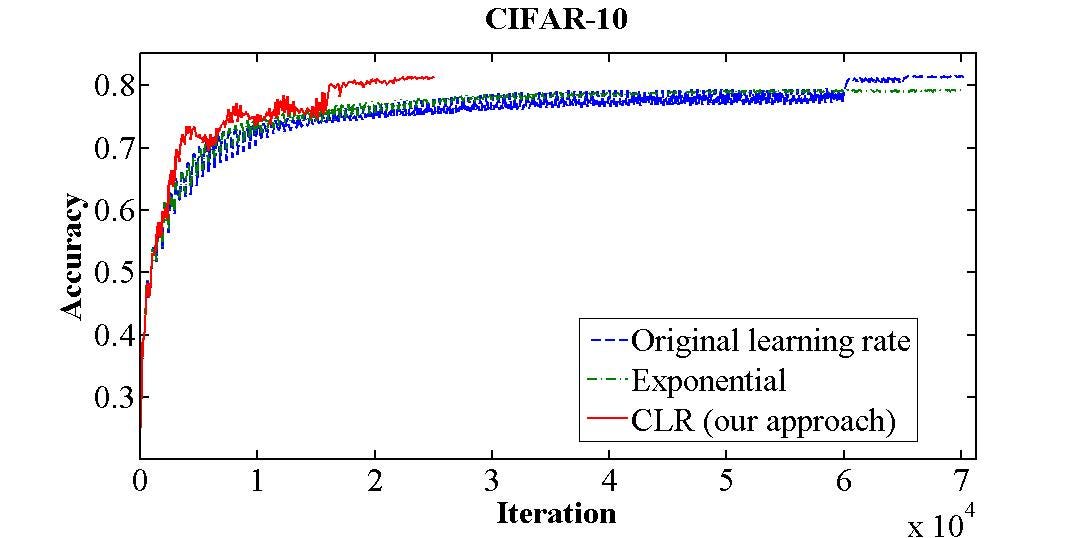
Figure 2. Accuracy while training CIFAR-10, ruby line shows training with circadian learning rate. (image credits)

Information technology is also important to annotation that allowing learning rate to swing between range of values might harm the network temporarily but information technology is beneficial overall.

Okay, what about Adaptive learning rates then ?

Adaptive learning rate and Cyclical learning rate are two unlike approaches birthday. Say, they are similar competitors. Adaptive learning rate has a meaning computational cost in finding local adaptive route while cyclical learning rate does not posses this computational cost, a small amount of computation is saved here. Cyclical learning charge per unit being fundamentally unlike from adaptive learning rate, it can be used along with adaptive learning rate. Combining cyclical learning rate with adaptive technique wouldn't crave that significant computation mentioned above.

Cycling to about optimal point using Cyclical Learning Rate schedule.

Like mentioned in the beginning of this postal service, "this method cyclically vary betwixt reasonable boundary values". Boundary values here means in that location is 1 upper bound and one lower spring. Learning rate cyclically varies between these bounds.

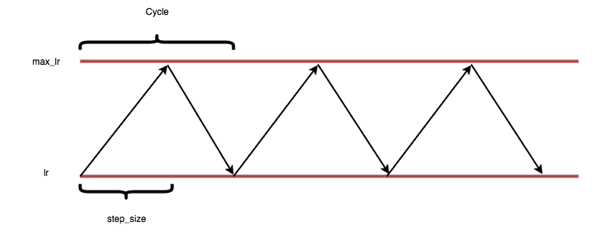
Figure 3. Pictorial representation of Cyclical Learning Charge per unit. (image credits)

As you can run into,

max_lr = maximum boundary
lr = minimum purlieus
step_size = is basically half a cycle
Cycle = ane consummate linear increment and decrease.

Flavors of Cyclic Learning Charge per unit.

Triangular Schedule.

Triangular schedule has fixed minimum and maximum boundaries beyond the cycles. Means at that place volition be no change to the max_lr and lr values till the terminate of all cycles.

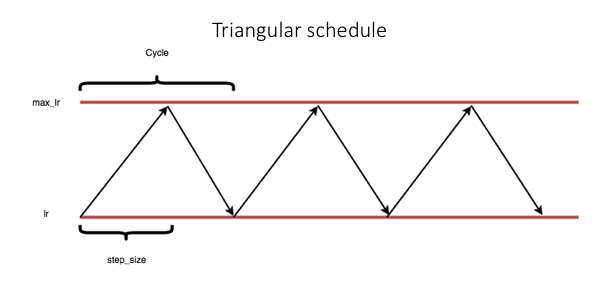
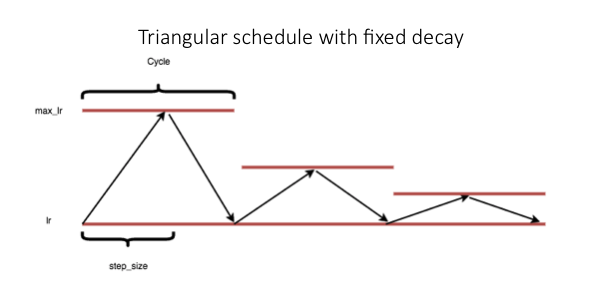
Triangular2 Schedule.

It is the same as the triangular policy except the learning rate difference is cut in one-half at the end of each cycle. This means the learning rate difference drops to one-half after each cycle.

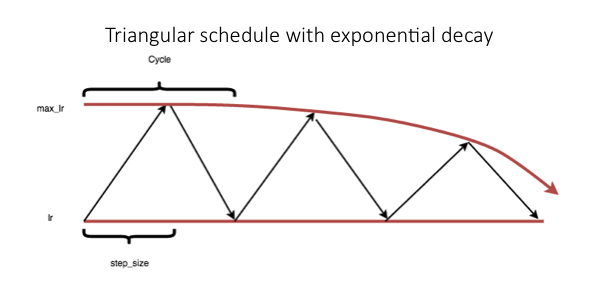
Exp Range.

The learning rate varies between the minimum and maximum boundaries and each boundary value declines by an exponential factor of gammaᶦᵗᵉʳᵃᵗᶦᵒⁿ.

How to observe values for minimum and maximum boundary ?

A elementary and straight frontward approach is to run the model for several iterations while letting the learning charge per unit increment linearly between depression and high LR values (typically between 0–0.1). Step size and max iteration should be fix to the same value before running the test. In this instance, learning charge per unit will increase linearly from the minimum value to the maximum value during the LR test run. Now record the learning rate and the accuracy, plot them and observe the value with which the accuracy starts to increase and the value when the accuracy drops or starts to autumn.

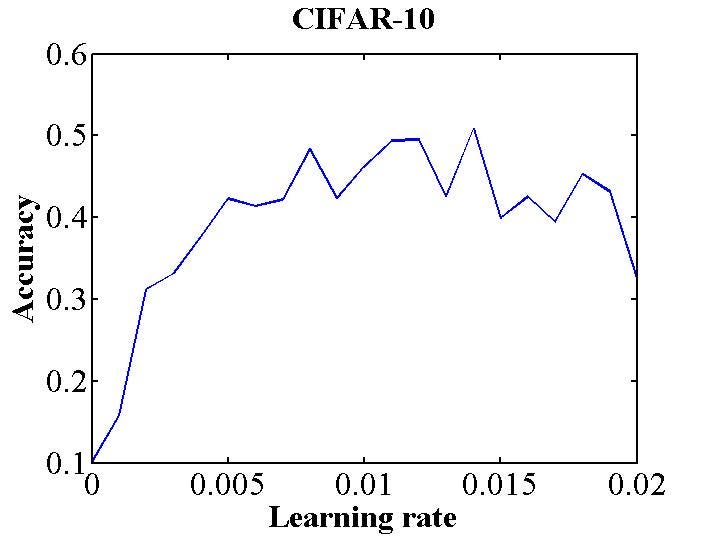
Effigy 7. LR Range test to find learning rate boundaries. (epitome credits)

In the effigy above you tin encounter that accuracy starts to increase right abroad at 0.001 and it dampens around 0.006, then these values will be good for minimum and maximum boundary values.

How to estimate good value for the cycle length ?

Run across step size in the in a higher place picture ? Yep that handles the cycle length value. As you lot have seen step size is but ane half of the wheel length. Over again it is important to note that iteration is used here instead of epoch eg., if CIFAR-10 has 50,000 training images and if batch size is 100 so it would have fifty,000/100 = 500 iterations.

According to the experiments past Leslie, it is often good to gear up step size equal to 2–8 times the no the iterations in an epoch. Running for more than than 4 cycles volition always give amend performance. Also it is best to stop training at the end of a cycle, which is when the learning rate is at the minimum value and the accuracy peaks.

Experiment has to say something.

Figure 8. CLR method achieves the same accurateness (cerise bend) within
25,000 iterations. (epitome credits)

With the Cyclical Learning Rate method it is possible to achieve an accurateness of 81.4% on the CIFAR-10 exam set within 25,000 iterations rather than 70,000 iterations using the standard learning rate. Settings for the above experiment are step size of 2,000, minimum and maximum is set to 0.001 and 0.006 respectively. Trinagular2 technique was used in the above experiment.

Leslie has fabricated clear that reducing the learning charge per unit doesn't actually help cyclical learning charge per unit policy, considering that is when the accurateness climbs the most. As a exam, a decay policy was implemented in which learning rate was decreased linearly from maximum to minimum bound(0.001 to 0.007) for a step size of 2,000 and from there learning rate was set up to minimum learning rate. This decay setting was simply able to accomplish 78.5% providing evidence that both increasing and decreasing the learning rate are essential for the benefits of the cyclical learning charge per unit method.

He has likewise tested Cyclical Learning Charge per unit with architectures like ResNets, Stochastic Depth and DenseNets it is axiomatic that cyclical Learning Rate gives a improve accuracy or on par at least. Cyclical Learning Charge per unit was also able to do better or on par with ImageNet models like AlexNet and GoogLeNet.

Conclusion.

In this post you would take got an idea about Cyclical Learning Rate, in the side by side postal service of this Learning Rates for Neural Neworks series you volition get to know virtually another impressive work past Ilya Loshchilov named Stochastic Gradient Descent with Warm Restarts.