What Is Entropy Machine Learning

scikit-acquire : Decision Tree Learning I - Entropy, Gini, and Information Gain

bogotobogo.com site search:

Determination Tree Learning

From wiki

Conclusion tree learning uses a decision tree as a predictive model which maps observations well-nigh an particular to conclusions almost the detail's target value.

It is ane of the predictive modelling approaches used in statistics, data mining and machine learning. Tree models where the target variable can take a finite gear up of values are called nomenclature trees. In these tree structures, leaves correspond form labels and branches stand for conjunctions of features that lead to those class labels. Decision trees where the target variable can take continuous values (typically existent numbers) are called regression trees.

In decision analysis, a decision tree can exist used to visually and explicitly correspond decisions and decision making. In data mining, a decision tree describes data but not decisions; rather the resulting classification tree can exist an input for decision making.

Impurity - Entropy & Gini

There are three commonly used impurity measures used in binary conclusion trees: Entropy, Gini index, and Nomenclature Error.

Entropy (a fashion to measure impurity):

$$ Entropy = -\sum_jp_j\log_2p_j$$

Gini index (a criterion to minimize the probability of misclassification):

$$ Gini = i-\sum_jp_j^2$$

Classification Fault:

$$ Classification Mistake = one-\max p_j$$

where $p_j$ is the probability of class $j$.

The entropy is 0 if all samples of a node belong to the same form, and the entropy is maximal if we have a uniform form distribution. In other words, the entropy of a node (consist of single class) is cypher because the probability is one and log (i) = 0. Entropy reaches maximum value when all classes in the node take equal probability.

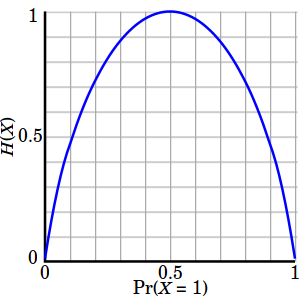
Entropy of a group in which all examples belong to the aforementioned class: $$ entropy = -1 \log_2 1 = 0 $$ This is not a skilful set for training.
entropy of a grouping with fifty% in either class:

So, basically, the entropy attempts to maximize the mutual data (past amalgam a equal probability node) in the decision tree.

Similar to entropy, the Gini index is maximal if the classes are perfectly mixed, for example, in a binary class:

$$ Gini = 1 - (p_1^2 + p_2^2) = 1-(0.five^2+0.5^2) = 0.5$$

Information Gain (IG)

Using a conclusion algorithm, nosotros starting time at the tree root and split the information on the characteristic that results in the largest information gain (IG).

We repeat this splitting procedure at each kid node down to the empty leaves. This means that the samples at each node all vest to the same grade.

However, this can result in a very deep tree with many nodes, which can easily lead to overfitting. Thus, nosotros typically want to prune the tree by setting a limit for the maximum depth of the tree.

Basically, using IG, we want to determine which aspect in a given prepare of preparation feature vectors is most useful. In other words, IG tells us how important a given attribute of the characteristic vectors is.

We will use it to decide the ordering of attributes in the nodes of a conclusion tree.

The Data Proceeds (IG) can be defined as follows:

$$ IG(D_p) = I(D_p) - \frac{N_{left}}{N_p}I(D_{left}) - \frac{N_{right}}{N_p}I(D_{right})$$

where $I$ could exist entropy, Gini alphabetize, or classification error, $D_p$, $D_{left}$, and $D_{right}$ are the dataset of the parent, left and right child node.

Information Gain (IG) - Examples

In this section, we'll go IG for a specific example as shown below:

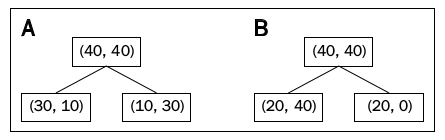
First, IG with Classification Error ($IG_E$):

$$ Classification Error = 1-\max p_j$$ $$ I_E(D_p) = 1 - \frac{40}{80} = ane - 0.5 = 0.v $$ $$ A:I_E(D_{left}) = 1 - \frac{30}{xl} = 1 - \frac34 = 0.25 $$ $$ A:I_E(D_{correct}) = 1 - \frac{thirty}{40} = 1 - \frac34 = 0.25 $$ $$ IG(D_p) = I(D_p) - \frac{N_{left}}{N_p}I(D_{left}) - \frac{N_{right}}{N_p}I(D_{right})$$ $$ A:IG_E = 0.five - \frac{40}{fourscore} \times 0.25 - \frac{40}{80} \times 0.25 = 0.v - 0.125 - 0.125 = \colour{bluish}{0.25}$$ $$ B:I_E(D_{left}) = ane - \frac{40}{60} = 1 - \frac23 = \frac13 $$ $$ B:I_E(D_{right}) = i - \frac{20}{xx} = ane - ane = 0 $$ $$ B:IG_E = 0.5 - \frac{60}{fourscore} \times \frac13 - \frac{xx}{eighty} \times 0 = 0.5 - 0.25 - 0 = \colour{blue}{0.25}$$

The information gains using the classification mistake every bit a splitting criterion are the aforementioned (0.25) in both cases A and B.

IG with Gini alphabetize ($IG_G$):

$$ Gini = 1-\sum_jp_j^2$$ $$ I_G(D_p) = 1 - \left( \left(\frac{40}{80} \right)^two + \left(\frac{forty}{fourscore}\right)^2 \right) = 1 - (0.5^two+0.5^two) = 0.5 $$ $$ A:I_G(D_{left}) = 1 - \left( \left(\frac{xxx}{forty} \correct)^2 + \left(\frac{ten}{40}\right)^2 \right) = 1 - \left( \frac{ix}{sixteen} + \frac{1}{16} \right) = \frac38 = 0.375 $$ $$ A:I_G(D_{correct}) = 1 - \left( \left(\frac{10}{xl}\right)^2 + \left(\frac{xxx}{40}\right)^2 \right) = i - \left(\frac{1}{16}+\frac{nine}{sixteen}\correct) = \frac38 = 0.375 $$ $$ A:I_G = 0.5 - \frac{40}{80} \times 0.375 - \frac{40}{fourscore} \times 0.375 = \color{bluish}{0.125} $$ $$ B:I_G(D_{left}) = i - \left( \left(\frac{xx}{sixty} \right)^2 + \left(\frac{40}{60}\right)^two \right) = 1 - \left( \frac{9}{sixteen} + \frac{one}{16} \right) = i - \frac59 = 0.44 $$ $$ B:I_G(D_{correct}) = 1 - \left( \left(\frac{twenty}{20}\right)^2 + \left(\frac{0}{20}\right)^2 \correct) = 1 - (ane+0) = i - 1 = 0 $$ $$ B:I_G = 0.five - \frac{60}{80} \times 0.44 - 0 = 0.5 - 0.33 = \color{blueish}{0.17} $$

And so, the Gini index favors the split B.

IG with Entropy ($IG_H$):

$$ Entropy = -\sum_jp_j\log_2p_j$$ $$ I_H(D_p) = - \left( 0.5\log_2(0.v) + 0.5\log_2(0.5) \right) = i $$ $$ A:I_H(D_{left}) = - \left( \frac{30}{twoscore}\log_2 \left(\frac{30}{40} \right) + \frac{x}{40}\log_2 \left(\frac{ten}{40} \right) \right) = 0.81 $$ $$ A:I_H(D_{right}) = - \left( \frac{10}{40}\log_2 \left(\frac{10}{xl} \correct) + \frac{30}{twoscore}\log_2 \left(\frac{30}{twoscore} \right) \right) = 0.81 $$ $$ A:IG_H = 1 - \frac{40}{lxxx} \times 0.81 - \frac{40}{lxxx} \times 0.81 = \color{bluish}{0.xix} $$ $$ B:I_H(D_{left}) = - \left( \frac{20}{threescore}\log_2 \left(\frac{20}{60} \right) + \frac{forty}{60}\log_2 \left(\frac{40}{60} \correct) \right) = 0.92 $$ $$ B:I_H(D_{right}) = - \left( \frac{20}{20}\log_2 \left(\frac{twenty}{twenty} \correct) + 0 \right) = 0 $$ $$ B:IG_H = 1 - \frac{60}{80} \times 0.92 - \frac{20}{80} \times 0 = \color{blue}{0.31} $$

So, the entropy criterion favors B.

Information Gain (IG) - Examples

In this section, nosotros'll plot the three impurity criteria we discussed in the previous section:

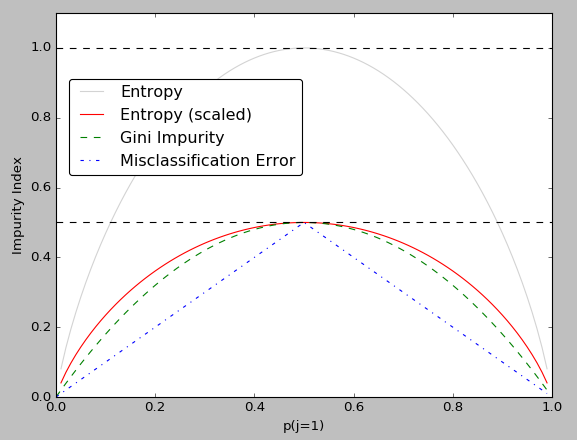
Annotation that we introduced a scaled version of the entropy (entropy/2) to emphasize that the Gini alphabetize is an intermediate measure between entropy and the classification error.

The code used for the plot is as follows:

import matplotlib.pyplot as plt import numpy as np  def gini(p):    render (p)*(1 - (p)) + (i - p)*(1 - (1-p))  def entropy(p):    render - p*np.log2(p) - (1 - p)*np.log2((1 - p))  def classification_error(p):    render 1 - np.max([p, one - p])  x = np.arange(0.0, 1.0, 0.01) ent = [entropy(p) if p != 0 else None for p in x] scaled_ent = [e*0.5 if east else None for e in ent] c_err = [classification_error(i) for i in 10]  fig = plt.figure() ax = plt.subplot(111)  for j, lab, ls, c, in zip(       [ent, scaled_ent, gini(x), c_err],       ['Entropy', 'Entropy (scaled)', 'Gini Impurity', 'Misclassification Mistake'],       ['-', '-', '--', '-.'],       ['lightgray', 'red', 'green', 'bluish']):    line = ax.plot(10, j, label=lab, linestyle=ls, lw=1, color=c)  ax.fable(loc='upper left', bbox_to_anchor=(0.01, 0.85),          ncol=1, fancybox=True, shadow=Simulated)  ax.axhline(y=0.5, linewidth=ane, color='yard', linestyle='--') ax.axhline(y=1.0, linewidth=i, color='thousand', linestyle='--')  plt.ylim([0, one.1]) plt.xlabel('p(j=i)') plt.ylabel('Impurity Index') plt.show()

Machine Learning with scikit-learn

scikit-acquire installation

scikit-learn : Features and characteristic extraction - iris dataset

scikit-learn : Auto Learning Quick Preview

scikit-learn : Data Preprocessing I - Missing / Categorical data

scikit-learn : Data Preprocessing 2 - Partitioning a dataset / Characteristic scaling / Feature Choice / Regularization

scikit-learn : Data Preprocessing III - Dimensionality reduction vis Sequential feature selection / Assessing feature importance via random forests

Data Compression via Dimensionality Reduction I - Primary component analysis (PCA)

scikit-learn : Information Compression via Dimensionality Reduction Ii - Linear Discriminant Analysis (LDA)

scikit-acquire : Data Compression via Dimensionality Reduction III - Nonlinear mappings via kernel primary component (KPCA) analysis

scikit-learn : Logistic Regression, Overfitting & regularization

scikit-acquire : Supervised Learning & Unsupervised Learning - due east.thou. Unsupervised PCA dimensionality reduction with iris dataset

scikit-learn : Unsupervised_Learning - KMeans clustering with iris dataset

scikit-learn : Linearly Separable Data - Linear Model & (Gaussian) radial basis role kernel (RBF kernel)

scikit-larn : Decision Tree Learning I - Entropy, Gini, and Data Proceeds

scikit-acquire : Decision Tree Learning Two - Constructing the Decision Tree

scikit-acquire : Random Decision Forests Classification

scikit-learn : Support Vector Machines (SVM)

scikit-learn : Back up Vector Machines (SVM) II

Flask with Embedded Machine Learning I : Serializing with pickle and DB setup

Flask with Embedded Machine Learning II : Basic Flask App

Flask with Embedded Machine Learning Iii : Embedding Classifier

Flask with Embedded Car Learning Iv : Deploy

Flask with Embedded Auto Learning V : Updating the classifier

scikit-learn : Sample of a spam comment filter using SVM - classifying a proficient one or a bad one

Motorcar learning algorithms and concepts

Batch gradient descent algorithm

Unmarried Layer Neural Network - Perceptron model on the Iris dataset using Heaviside step activation office

Batch gradient descent versus stochastic gradient descent

Single Layer Neural Network - Adaptive Linear Neuron using linear (identity) activation function with batch gradient descent method

Single Layer Neural Network : Adaptive Linear Neuron using linear (identity) activation role with stochastic gradient descent (SGD)

Logistic Regression

VC (Vapnik-Chervonenkis) Dimension and Shatter

Bias-variance tradeoff

Maximum Likelihood Estimation (MLE)

Neural Networks with backpropagation for XOR using ane subconscious layer

minHash

tf-idf weight

Natural language Processing (NLP): Sentiment Analysis I (IMDb & pocketbook-of-words)

Natural Language Processing (NLP): Sentiment Analysis Ii (tokenization, stemming, and finish words)

Natural Language Processing (NLP): Sentiment Analysis Three (training & cross validation)

Natural Language Processing (NLP): Sentiment Analysis Four (out-of-cadre)

Locality-Sensitive Hashing (LSH) using Cosine Distance (Cosine Similarity)

Artificial Neural Networks (ANN)

[Notation] Sources are available at Github - Jupyter notebook files

1. Introduction

two. Forward Propagation

3. Gradient Descent

iv. Backpropagation of Errors

v. Checking slope

six. Training via BFGS

7. Overfitting & Regularization

eight. Deep Learning I : Image Recognition (Image uploading)

9. Deep Learning II : Image Recognition (Image classification)

10 - Deep Learning III : Deep Learning Three : Theano, TensorFlow, and Keras

Source: https://www.bogotobogo.com/python/scikit-learn/scikt_machine_learning_Decision_Tree_Learning_Informatioin_Gain_IG_Impurity_Entropy_Gini_Classification_Error.php

Posted by: bergergaceaddly.blogspot.com